Integrated Mathematical Oncology Research

Translational Mathematical and Computational Oncology

Evolutionary Therapy

For many therapeutic protocols, the initial positive response is followed by the evolution of drug resistance and treatment failure. Rather than ignoring this evolution, evolutionary-enlightened therapeutic approaches deliberately embrace the dynamics that govern the emergence of drug resistance and develop treatment strategies that can exploit these dynamics. Evolutionary Therapy protocols developed at the IMO hold a promise to revolutionize personalized cancer therapy, making the treatment response of an individual patient the driver of their own treatment schedule.

IMO Mathematical Models & Tools

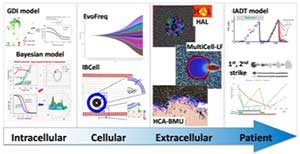Various quantitative computational models that support in vitro and in vivo experiments, ex vivo data analyses, and clinical treatment design have been developed by the IMO. Several mathematical techniques are being used, including continuous ODEs and PDEs; individual cell-based models, such as hybrid cellular automata, multi-cell force-based models, and fluid-structure interactions models; game theory; stochastic models; machine learning and optimization techniques; and Bayesian models. These approaches span several biological scales: from genes and proteins to cells, cell clones, and tissue turnover, the surrounding microenvironment and metastatic colonization of distant sites, to modeling the whole tumor response to treatments. IMO models are parameterized with experimental and clinical data from collaborating laboratories, and used to predict tumor response to anti-cancer therapies.

Quantitative Personalized Oncology

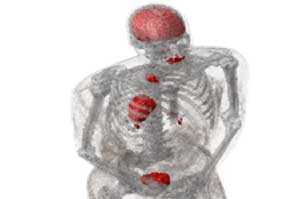Integrative mathematical models are being developed for a particular clinical problem and used to predict patient-specific treatment responses, with the ultimate aim of assisting clinical decision making on a per-patient basis. the focus of IMO is on models that can be informed with routinely collected clinical data and can simulate clinically approved treatments, protocols, and combination therapies. Simple mathematical models are trained using retrospective clinical data to derive parameter distributions for each participating mechanism. Those with small variations are collapsed into uniform rate constants, while the remaining parameters most likely determine patient-specific outcomes. Calibrated models are validated on independent training data before virtual in silico trials will determine optimal treatment protocols on a per-patient basis.

Bone Cancer Ecosystem and Evolution

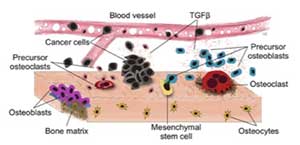Genetic mutations are associated with tumor initiation and fuel somatic evolution, but the selection process results from the interactions between the different clonal populations that emerge in the bone ecosystem. By developing mathematical models that capture these dynamic aspects and characterize tissue ecology, IMO aims to understand the drivers of tumor progression, with a goal to determine novel treatment strategies that take those evolutionary and ecological dynamics into account.

Adaptive Therapy

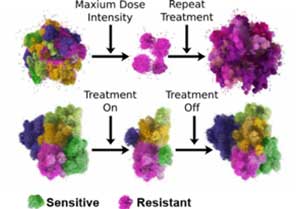In contrast to a common maxim in cancer “hit hard and fast”, the IMO approach is to only treat a subset of the tumor, ensuring that a drug-sensitive population is left behind when treatment stops, allowing it to regrow. The timing of each treatment is thus adapted to each individual patient’s cancer—how tumors respond to the initial treatment will dictate when the treatment should stop and when the next round should begin.  

Radiotherapy Modeling

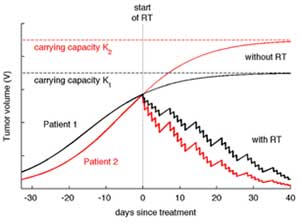Although radiation is widely used as a treatment, most scheduling is based on empirical knowledge. The IMO develops quantitative models for radiotherapy response in vitro, in vivo, and in patients, with and without concurrent immunotherapy. The objective is to study responses on the single-cell level, different fractionated treatment protocols, and targeted intraoperative radiotherapy. The long-term goal is to develop precision radiation oncology together with Moffitt clinicians that can reduce mortality and improve the quality of life of patients.

Micro-pharmacology

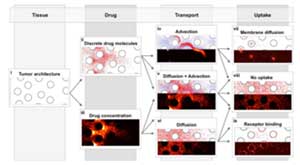Systemic chemotherapy is one of the main anticancer treatments used for clinically diagnosed tumors. However, its main impediment is that the therapeutic agents must reach all tumor cells in sufficient quantities. IMO develops models to examine ways of improving drug delivery on a cell-to-tissue scale (micro-pharmacology, microPKPD), that take into account drug interstitial transport, tumor irregular cellular and fibril architecture, and dynamic spatio-temporal changes in a tumor microenvironment.

Quantification of Intra-tumor Heterogeneity

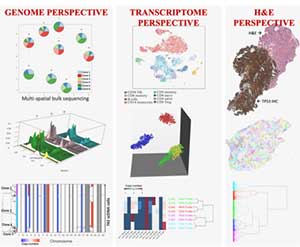Tumors can adapt to treatments because they are heterogeneous, though the relative frequencies of different tumor subclones can change in response to treatment. Cellular diversity can be quantified in various ways: taking advantage of single-cell sequencing (sc-Seq), looking at the cell’s RNA instead of the DNA, at imaging data, and at the cells' microenvironment. Each method will likely present a different population structure. However, for clinical applications, the outline of subpopulations that defines differential drug sensitivities would be most desired. Data integration is likely to bring us closer to this goal than looking only at a single angle. The models developed at IMO aim at integrating multiple perspectives to better answer the question: What really is a clone? This will provide a powerful metric of tumor evolution parameters that are otherwise difficult to measure directly. The ultimate goal is to investigate temporal changes in the clonal composition in the face of defined selective pressures, such as DNA-damaging therapies or nutrient limitations.

In Silico Tumor Organoids

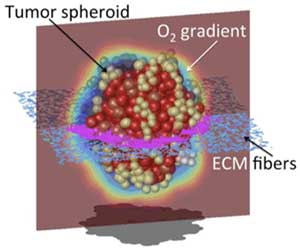Primary tumors and tumor metastases grow as three-dimensional (3D) masses of cells within a specific tumor microenvironment. Tumor organoids are 3D experimental cultures that mimic the growth of in vivo tumors and their response to treatments. IMO develops in silico tumor organoid models that reconstruct tumor cellular and microenvironmental heterogeneities, and can be used to examine, in a reproducible and quantitative way, how tumor morphology, the composition and structure of the surrounding stroma, and variable metabolic gradients influence the efficacy of anticancer treatments, including chemotherapy, targeted therapy, radiotherapy and immunotherapy. These models can also be personalized to recapitulate the pathophysiological features of patient-derived organoids and tumors.